Momentan belege ich an der Uni eine sehr interessante Vorlesung über Zellularautomaten. Ich möchte in den nächsten Artikeln ein paar sehr interessante Aspekte aufzeigen, sollte aber vorher ein paar Grundlagen schaffen.
Ein Zellularautomat besteht aus Zellen (sehr intuitiv, ich weiß). Die Idee dahinter ist, dass alle Zellen (bei geeigneter Abstraktion) gleich sind, sich also identisch verhalten. Eine Zelle hat eine gewisse Anzahl an Nachbarzellen. Anhand des eigenen Zustands und des Zustands der unmittelbaren Nachbarzellen wird das Verhalten einer Zelle festgelegt. In jedem “Rechenschritt” werden alle Zellen zu einem bestimmten Zeitpunkt t betrachtet und der Zustand für den Zeitpunkt t+1 für alle Zellen parallel berechnet. Im Großen und Ganzen war es das auch schon, nur sind Beispiele in der Regel spannender.
Ein sehr bekanntes und beliebtes Beispiel ist Conways Game of Life. Wir betrachten hier einen Zellularraum mit zwei Dimensionen. Alle Zellen haben genau 8 Nachbarzellen (vergleichbar mit einem Kästchen auf Karopapier). In diesem Zellularraum kann eine Zelle nur zwei Zustände annehmen (in diesem Fall tot oder lebendig). Die Regeln für diesen Zellularraum sind denkbar einfach:
- hat eine tote Zelle genau drei lebende Nachbarzellen, wird sie im nächsten Zeitabschnitt geboren.
- hat eine lebende Zelle weniger als zwei lebende Nachbarzellen, so stirbt sie an Einsamkeit.
- hat eine lebende Zelle mehr als drei lebende Nachbarzellen, so stirbt sie an Überbevölkerung.
- in jedem anderen Fall passiert nichts.
Das waren auch schon alle Regeln. Die interessierten theoretischen Informatiker bekommen an dieser Stelle gerne gesagt, dass man damit eine Turingmaschine simulieren kann, also alle rekursiv aufzählbaren Funktionen berechnen kann. Für die Nichtinformatiker: Man kann damit alles machen, was man mit einem Computer auch machen kann.
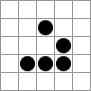
Kommen wir zu einem Beispiel: Betrachten wir folgenden Zellenausschnitt:
Einigen kommt diese Anordnung vielleicht bekannt vor. Es handelt sich dabei um das Hacker-Emblem.
Betrachten wir nun was mit dieser Zellanordnung passiert, indem wir die Regeln auf diese 25 Zellen anwenden. Die Reihenfolge der Abarbeitung ist egal, weil die Berechnung parallel geschieht. Mit (x,y) bezeichne ich die Zelle in Spalte x und Zeile y:
- (1,1) mit 0 lebenden Nachbarzellen nimmt den Zustand tot an.
- (1,2) mit 0 lebenden Nachbarzellen nimmt den Zustand tot an.
- (1,3) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (1,4) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (1,5) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (2,1) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (2,2) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (2,3) mit 3 lebenden Nachbarzellen nimmt den Zustand lebend an.
- (2,4) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (2,5) mit 2 lebenden Nachbarzellen nimmt den Zustand tot an.
- (3,1) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (3,2) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (3,3) mit 5 lebenden Nachbarzellen nimmt den Zustand tot an.
- (3,4) mit 3 lebenden Nachbarzellen nimmt den Zustand lebend an.
- (3,5) mit 3 lebenden Nachbarzellen nimmt den Zustand lebend an.
- (4,1) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (4,2) mit 2 lebenden Nachbarzellen nimmt den Zustand tot an.
- (4,3) mit 3 lebenden Nachbarzellen nimmt den Zustand lebend an.
- (4,4) mit 2 lebenden Nachbarzellen nimmt den Zustand tot an.
- (4,5) mit 2 lebenden Nachbarzellen nimmt den Zustand tot an.
- (5,1) mit 0 lebenden Nachbarzellen nimmt den Zustand tot an.
- (5,2) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (5,3) mit 2 lebenden Nachbarzellen nimmt den Zustand tot an.
- (5,4) mit 2 lebenden Nachbarzellen nimmt den Zustand tot an.
- (5,5) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
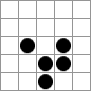
Daraus ergibt sich in der nächsten “Generation” folgende Konfiguration:
Auf diese Konfiguration wenden wir die Regeln ebenfalls an:
- (2,3) mit 1 lebenden Nachbarzelle nimmt den Zustand tot an.
- (2,4) mit 3 lebenden Nachbarzellen nimmt den Zustand lebend an.
- (3,4) mit 4 lebenden Nachbarzellen nimmt den Zustand tot an.
- (4,5) mit 3 lebenden Nachbarzellen nimmt den Zustand lebend an.
- alle anderen Zellen behalten ihren Zustand bei.
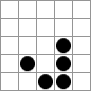
Dadurch erhalten wir folgende Konfiguration:
Dieses Spielchen kann man ewig so weiter treiben. Man erkennt, dass sich dieses Gebilde nach rechts unten bewegt. Würden wir noch zwei weitere Generationen berechnen, so erhielten wir die ursprüngliche Konfiguration um (2,2) verschoben. Die Figur wird auch Gleiter genannt, weil sie durch den Zellularraum gleitet.
Im nächsten Artikel zu Zellularautomaten werde ich entweder die Gleiterkanone oder den Gleider-Fresser vorstellen. Mit diesen beiden Gebilden und dem Gleiter kann man bereits etwas sehr spannendes konstruieren, jedoch werde ich noch nicht verraten was.